Cari colleghe, cari colleghi,
vi propongo un tipo di attività didattica ispirata alla Practice Relay, organizzata dal CEMC – Centre for Education in Mathematics and Computing dell’Università di Waterloo in Canada.
In pratica è un gioco a squadre basato su problemi abbastanza facili che funziona così, nella mia proposta:
- Ogni squadra è formata da 5 studenti, numerati da 1 a 5.
L’obiettivo della squadra è quello di risolvere 5 problemi matematici e rispondere a una domanda finale. - A ciascun giocatore è assegnato un problema numerato da 1 a 5, corrispondente al proprio numero..
- Inizia il giocatore 1 che risolve il problema 1.
- Una volta ottenuta la risposta, la consegna al giocatore 2, che ne ha bisogno per risolvere il problema 2.
- Questo processo continua in sequenza: ogni giocatore dipende dalla risposta del precedente per risolvere il proprio problema.
- La staffetta termina quando il giocatore 5 consegna la risposta finale.
Lo spirito del gioco
Nella mia proposta, lo spirito del gioco dovrebbe essere la collaborazione e la strategia piuttosto che la competizione e la velocità.
Per favorire questo approccio, si potrebbe ammettere lo scambio di problemi tra i giocatori e la possibilità di lavorare in anticipo sul proprio problema prima ricevere la risposta di quello precedente.
Smontate il gioco e cambiate le regole
Se questa attività vi piace, smontatela, cambiate le regole e ricostruitela in base alle esigenze delle vostre classi.
Ecco alcune possibili varianti.
- Condivisione dei problemi. Il gruppo riceve tutti i 5 problemi e decide insieme come organizzarsi.
- Gruppi flessibili. Anche coppie o piccoli gruppi possono partecipare, adattando la staffetta alle proprie dinamiche.
- Modalità individuale. Un singolo studente può affrontare l’intera serie con più tempo a disposizione, esercitando autonomia e concentrazione.
Un esempio
Problema 1
Quanto vale la SOMMA dei risultati delle seguenti espressioni?
14 – 2 × 3 + 10 : 2
(14 – 2 × 3 + 10) : 2
Consegna il risultato al giocatore 2.
Problema 2
Chiama A il risultato che hai ricevuto e sostituiscilo nel problema seguente.
Quanti sono i numeri dispari nella lista seguente?
1, 3, 5, 9, 18, A, 25, (A+9), 170, 171, (A+990)
Consegna il risultato al giocatore 3.
Problema 3
Chiama B il risultato che hai ricevuto e sostituiscilo nel problema seguente.
Tutti i lati consecutivi del poligono disegnato qui sotto si incontrano perpendicolarmente fra loro.
I numeri indicano le lunghezze dei lati in centimetri.
Quanto misura il suo perimetro?
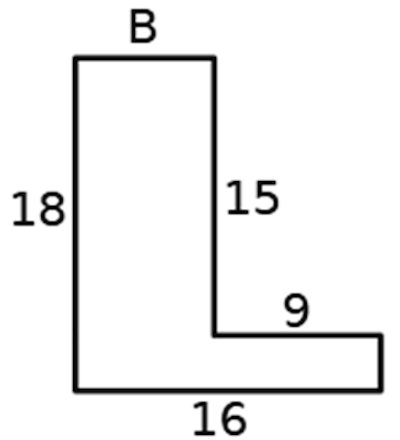
Consegna il risultato al giocatore 4.
Problema 4
Chiama C il risultato che hai ricevuto e sostituiscilo nel problema seguente.
Un autobus parte con C persone a bordo.
Alla prima fermata, 15 persone scendono e 3 persone salgono.
Alla seconda fermata, 7 persone salgono e 21 persone scendono.
Calcola il numero di persone presenti sull’autobus quando riparte dopo la seconda fermata.
Consegna il risultato al giocatore 5.
Problema 5
Chiama D il risultato che hai ricevuto e sostituiscilo nel problema seguente.
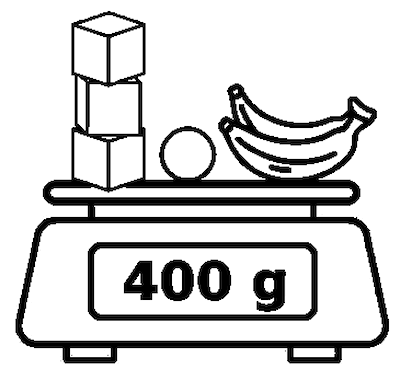
La figura mostra una bilancia con alcuni oggetti sul piatto.
Se ogni cubo pesa D grammi e la pallina pesa 24 grammi, quanto pesa una banana?
Chiama E il risultato. Quanto vale E?
Risposte & riflessioni
Ecco la soluzione in breve ma…
questa serie di problemi a staffetta contiene un piccolo trucco… che vedremo subito dopo.
———————————-
Problema 1.
Risposta: 22
———————————-
Problema 2.
Input: A = 22
Risposta: 7
———————————-
Problema 3.
Input: B = 7
Risposta: 68
———————————-
Input: C = 68
Risposta: 42
———————————-
Input: D = 42
Risposta: 125 (attenzione: le banane sono due)
Quindi la risposta finale è:
E = 125
———————————-
Come dicevo, questa serie di problemi a staffetta contiene un piccolo trucco. Se gli studenti lo scoprono e lo usano per migliorare la collaborazione, è un bel risultato.
Riprendiamo il problema 3
Problema 3
Chiama B il risultato che hai ricevuto e sostituiscilo nel problema seguente.
Tutti i lati consecutivi del poligono disegnato qui sotto si incontrano perpendicolarmente fra loro.
I numeri indicano le lunghezze dei lati in centimetri.
Quanto misura il suo perimetro?
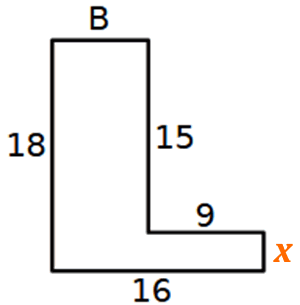
Consegna il risultato al giocatore 4.
———————————-
Ok, B = 7, e si può ricavare il valore di x per differenza:
x = (18-15) = 3 cm.
Quindi il perimetro del poligono vale:
18 + B + 15 + 9 + 3 + 16
= 18 + 7 + 15 + 9 + 3 + 16
= 68 cm
Ma il perimetro del poligono si può trovare anche senza conoscere né B né x!
E non servono neppure i valori 15 e 9.
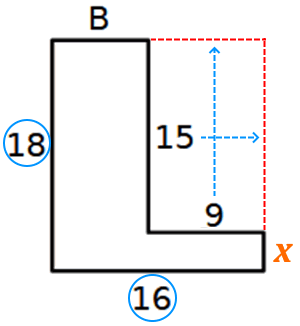
Infatti basta traslare i segmenti lunghi 15 cm e 9 cm per ottenere un rettangolo di dimensioni 16 cm e 18 cm.
Tale rettangolo ha il perimetro uguale a quello del poligono di partenza, cioè:
(18 + 16) × 2 = 68 cm.
—
Pace e bene a tutti.
GfBo
Foto cover: beeboys / Shutterstock
Ilustrazioni: Gianfranco Bo
L’articolo è pubblicato anche su BASE Cinque.


