Affrontare un problema matematico diventa un’esperienza potente quando ti consente di esplorare la tua rete di conoscenze personali. Di diventarne consapevole. Di espanderla. Credo che per un Matematico sia una sorta di esercizio spirituale.
Problema 1. Numeri sui vertici di un cubo
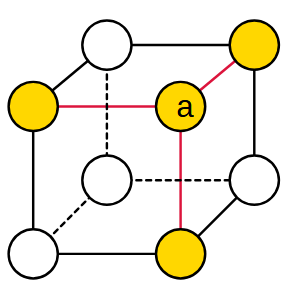
Assegna un numero da 0 a 7, senza ripetizioni, a ciascun vertice di un cubo in modo tale che la somma degli estremi di ogni spigolo sia un numero primo.
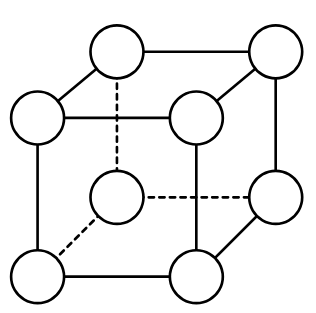
Ecco un tentativo di soluzione parziale che rispetta le condizioni. Ma NON è la soluzione corretta.
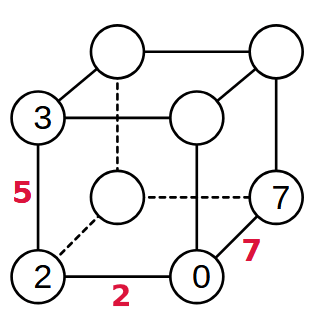
Pensieri a ruota libera
Non metterti subito all’opera per risolvere il problema, prima esplora le aree della tua rete personale di conoscenze che si accendono alla lettura del problema. Anche quelle più elementari!
Ti propongo qualche spunto che potrebbe essere diverso dai tuoi perché ciascuno ha una rete di conoscenze personale e unica.
- Numeri. Contare da 0 a 7. Contare? Zero?
- Addizione, somma. Proprietà commutativa?
- Combinazioni. In quanti modi posso rappresentare un numero primo come somma di due numeri naturali? No, non c’entra con la congettura di Goldbach!
- Numeri primi. Mattoni fondamentali dell’Aritmetica.
- Cubo, vertici, spigoli. Siamo in geometria? Oppure parliamo di grafi?
- Grafi. Un cubo ha 3 dimensioni, ma il suo grafo potrebbe averne solo 2?
- Collegamenti. Ogni vertice quanti collegamenti ha con altri vertici?
- Rappresentazione. Come rappresentare il grafo senza fare un disegno?
- Complessità. È un problema combinatorio? Quanto è complesso?
- Informatica. Potrei trovare tutte le soluzioni con un programmino? E come faccio?
E così via.
Vediamo alcuni aspetti indispensabili per risolvere il problema.
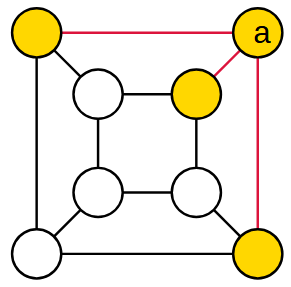
Il grafo planare del cubo
Se vuoi cercare la soluzione lavorando su una figura, conviene usare una rappresentazione planare del cubo. È più facile da verificare.
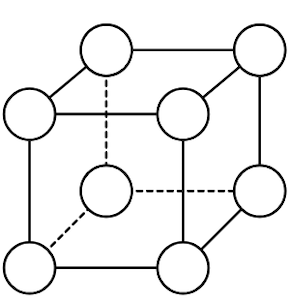
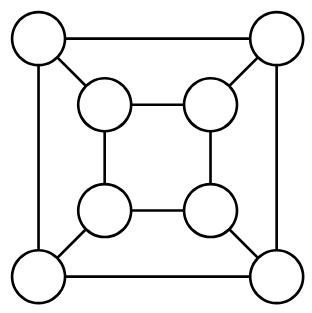
È importante osservare che ogni vertice è collegato con altri tre vertici.
Rappresentare un numero come somma di due primi
Visto che ogni vertice è collegato ad altri tre, bisogna controllare una condizione necessaria affinché il problema sia risolvibile.
Scrivi tutte le coppie che hanno come somma un numero primo e verifica che ogni numero da 0 a 7 compaia in almeno tre coppie.
| Somma | Coppie |
| 2 | (0,2) |
| 3 | (0,3), (1,2) |
| 5 | (0,5), (1,4), (2,3) |
| 7 | (0,7), (1,6), (2,5), (3,4) |
| 11 | (4,7), (5,6) |
| 13 | (6,7) |
Altre domande sul problema 1
Ecco tre possibili domande, ma tu potresti averne molte altre.
- Quante soluzioni diverse ha questo problema?
- Come posso trovare tutte le soluzioni scrivendo un programma per computer?
- Se risolvo questo problema con l’Intelligenza artificiale, cosa posso imparare di nuovo per me?
Problema 2. Facce costanti
Prova ad affrontare questo problema con lo stesso spirito di quello precedente.
Etichetta i vertici di un cubo con i numeri 1, 2, 3, 4, 5, 6, 7, 8 senza ripetizioni, in modo che la somma dei numeri ai quattro vertici di ciascuna faccia sia costante.

Altre domande sul problema 2
a) Quale deve essere l’unica somma possibile dei numeri su ciascuna faccia del cubo?
b) Quante soluzioni distinte ha il problema, a meno di rotazioni del cubo?
—
Nota.
L’ispirazione per questo articolo è nata da due problemi che ho trovato nel libro di Paul Yiu, Recreational Mathematics, Department of Mathematics, Florida Atlantic University, 2003.
PS: abbiamo pubblicato anche la soluzione!
Foto cover: Boryana Manzurova / Shutterstock
Ilustrazioni: Gianfranco Bo
L’articolo è pubblicato anche su BASE Cinque.


