La settimana scorsa vi ho proposto tre problemi epistemici molto semplici che vi permetteranno di capire meglio di cosa si tratta, apprezzarne il valore didattico e avere una base per approfondire l’argomento, se vi interessa.
Il più semplice problema epistemico con forme geometriche
Dov’è il premio?
Carlo e Sofia partecipano a un gioco matematico.
Il premio è nascosto in una delle scatole seguenti. Ogni scatola è identificabile in base a due caratteristiche: forma e colore.

Vince chi indovina per primo in quale scatola si trova il premio.
- A Sofia viene rivelata privatamente solo la forma della scatola contenente il premio.
- A Carlo viene rivelato privatamente solo il colore della scatola.
- Sofia sa che Carlo conosce il colore, Carlo sa che Sofia conosce la forma.
- Sofia e Carlo ragionano in modo perfettamente logico.
Il presentatore chiede: “Qualcuno di voi sa dov’è il premio?”
- Sofia e Carlo rispondono: “Non so dove è il premio.”
- Dopo un po’, però, Sofia e Carlo esclamano contemporaneamente: “Ora so dov’è il premio!”
Come si spiega?
Tu lo sai ora dov’è il premio?
L’avete risolto? Ecco la soluzione!
Per risolvere il problema dobbiamo metterci nei panni alternativamente di Sofia e di Carlo con lo scopo di ricavare tutte le informazioni possibili dalle loro dichiarazioni.
È utile, per prima cosa, mettere in ordine i pacchi in base alla forma e al colore.
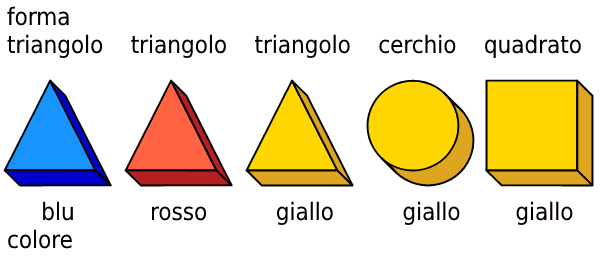
Ora analizziamo la prima dichiarazione di Sofia e Carlo: “Non so dove è il premio.”
- Mettiamoci nei panni di Sofia.
Sofia conosce la forma della scatola. Se la forma fosse un Cerchio o un Quadrato allora Sofia saprebbe dove è il premio. Se dichiara che non lo sa, allora il premio è in una scatola triangolare. - Mettiamoci nei panni di Carlo.
Carlo conosce il colore della scatola, se il colore fosse Blu oppure Rosso allora Carlo saprebbe dove è il premio. Se dichiara che non lo sa, allora il premio è in una scatola gialla.
In conclusione, il premio è in una scatola triangolare e gialla. Poiché c’è una sola scatola con entrambe le caratteristiche, sappiamo dov’è il premio!
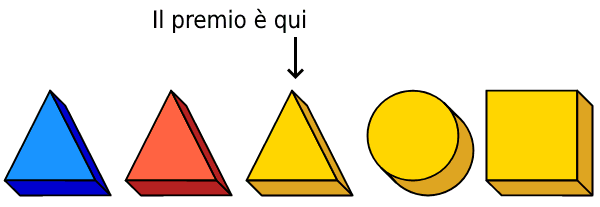
Sofia e Carlo fanno, ciascuno per conto proprio, gli stessi ragionamenti che abbiamo fatto noi, perciò dopo un po’ esclamano: “Ora so dov’è il premio!”
—
Osservazione importante: noi siamo riusciti a capire dove è il premio SENZA avere le informazioni private che avevano Carlo e Sofia. Ci sono bastate le loro dichiarazioni pubbliche di conoscenza: “non so…”, “ora so…”.
Il più semplice problema epistemico con numeri
Il numero più grande
Alice e Roberto hanno ricevuto ciascuno, privatamente, un biglietto con scritto un numero intero compreso fra 1 e 5 (1 ≤ n ≤ 5).

Alice e Roberto sanno che:
- ciascuno di essi conosce il proprio numero ma non quello dell’altra persona;
- i numeri scritti sui due biglietti sono interi, diversi fra loro e compresi fra 1 e 5.
Il compito di Alice e Roberto è quello di scoprire chi di loro ha il numero più grande.
Ecco il dialogo fra Alice e Roberto.
- Alice: “Non so qual è il numero maggiore.”
- Roberto: “Neanch’io so qual è il numero maggiore.”
- Alice: “Ora io lo so.”
- Roberto: “Ora io conosco entrambi i numeri.”
Avete capito quali sono i numeri scritti sui due biglietti?
E chi ha il numero più grande?
Spiegate come ci siete arrivati.
Lo avete risolto? Ecco la soluzione!
Per risolvere il problema dobbiamo metterci nei panni alternativamente di Alice e di Roberto con lo scopo di ricavare tutte le informazioni possibili dalle loro dichiarazioni pubbliche.
- Se Alice non sa qual è il numero più grande, allora non ha il numero 5.
- Se Roberto, dopo aver sentito Alice, non sa qual è il numero più grande, allora non ha né il 5, né il 4.
- Se Alice, a questo punto, ha capito qual è il numero maggiore, allora ha il numero 4 oppure il 3.
- Se Roberto, a questo punto ha capito quali sono entrambi i numeri, allora deve avere il 3 perché abbiamo dedotto sopra che non può avere né il 5 né il 4. Di conseguenza Alice ha il 4.
In conclusione: Alice = 4, Roberto = 3.
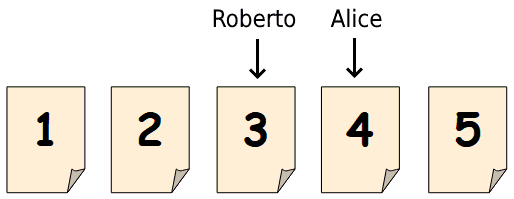
Il più semplice problema epistemico puramente logico

Cinque logici entrano in un bar.
La barista chiede: “Volete tutti una birra?”
- Primo logico: “Non lo so.”
- Secondo logico: “Non lo so.”
- Terzo logico: “Non lo so.”
- Quarto logico: “Non lo so.”
- Quinto logico: “No.”
La barista: “Ora so quante birre devo preparare.”
E voi lo sapete? Quante? Perché?
Cosa sarebbe successo se il quinto logico avesse risposto per primo?
Lo avete risolto? Ecco la soluzione!
La domanda della barista è: “Volete TUTTI una birra?”
La risposta “Non lo so” significa “Non so se TUTTI vogliamo birra” e non significa “Non so se IO voglio birra”.
Se per esempio il primo logico NON volesse una birra, risponderebbe “No” perché sarebbe certo che NON TUTTI vogliono birra.
Quindi il primo logico vuole una birra ma non sa se la vogliono tutti.
Stessa cosa per i seguenti tre logici.
L’ultimo logico non vuole una birra quindi risponde “No” per dire che NON TUTTI vogliono birra.
Ora la barista sa che dovrà preparare 4 birre.
—
Se l’ultimo logico avesse risposto per primo, avrebbe detto “No” e di conseguenza anche tutti gli altri avrebbero detto “No”. In questo caso la barista non avrebbe saputo quante birre preparare.
—
Se invece i logici volessero TUTTI una birra allora i primi quattro risponderebbero “Non lo so” e l’ultimo risponderebbe “Sì”.
Questo articolo è tratto dal sito BASE Cinque, di Gianfranco Bo, dove è distribuito nel pubblico dominio.
Foto cover: tadamichi / Shutterstock


